Exponentiële groei / vervalcalculator

Enter initial value (x0):  
Enter growth/decay rate (r): %
Enter time (t):  
   
Value at time t (x(t)):  

Exponentieel verval / groei is erg handig in Mathmatics. Exponentieel verval treedt op wanneer de groeipercentage negatief is. Exponentiële groei op dezelfde manier treedt op wanneer de groeipercentage van de waarde van een wiskundige functie evenredig is met de huidige waarde van de functie.

De formule voor exponentiële groei van een variabele X bij de (positieve of negatieve) groeisnelheid R, aangezien de tijd T doorgaat in discrete intervallen (dat wil zeggen op geheel getal 0, 1, 2, 3, ...), is < B> X T = X 0 (1 + R) T .

Waar X 0 de waarde van x is op tijdschroef 0. Wanneer de R negatieve ITIS-exponentieel verval is, wanneer de R positief is, is het exponentiële groei. Bijvoorbeeld, de groeisnelheid van R = 5% = 0,05, die van elke gehele tijdswaarde van tijd naar het volgende gehele getal veroorzaakt, veroorzaakt x op de tweede keer om 1,05 keer te zijn wat het in het vorige moment was.

Bijvoorbeeld, R = -0.5, de grafiek zal dalen (rottend). Elke keer dat T wordt verhoogd met 1, x t neemt af tot de helft van de vorige waarde.

Wanneer r = 1, is de grafiek groei. Elke keer dat T wordt verhoogd met 1, x t neemt toe met een factor 2.

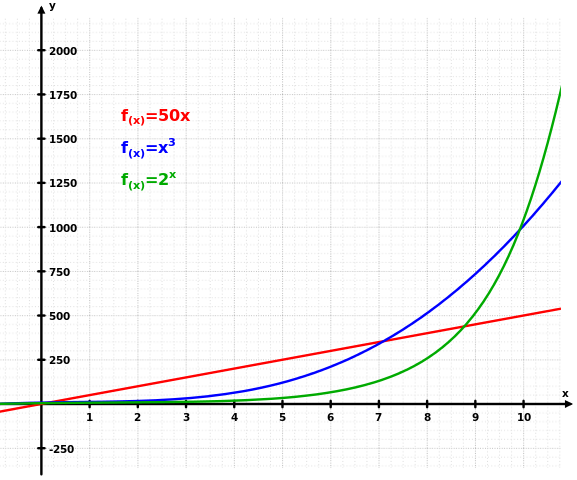
De grafiek illustreert hoe exponentiële groei (groen) zowel lineaire (rode) en kubieke (blauwe) groei overtreft.

Exponentiële groei / vervalcalculator
Aanbeveling rekenmachines Resolver desigualdades lineares Calculadora de distribuição hipergeométrica Calculadora de equação sexta Calculadora científica online. Efeito da calculadora de tamanho Equações de Transposição Resolvendo a calculadora Sinal para a calculadora de relação de ruído Calculadora do produto Cruz do vetor Calculadora de adição de vetor Calculadora de convolução online. Soma de calculadora consecutiva cubos Soma de calculadora de praças Soma de calculadora de quadrados consecutivos Calculadora de conjuntos de diferença simétrica Calculadora de teorema binômio