Eigenvectoren en eigevalues ​​berekening

Regular Matrix A =
Identity Matrix I =
Scalar Matrix(Z=c×I)
c =
|A| =
Singular Matrix (A - c×I) =
|A - c×I| =
Trace of A =
Eigen Value (c2) =
Eigen Value (c1) =
c1 in Eigen Vector x1 value =
c2 in Eigen Vector x1 value =
c1 in Eigen Vector x2 value =
c2 in Eigen Vector x2 value =

Een eigenVector van een vierkante matrix A is een niet-nulvector V, wanneer een V = λ V, de λ wordt genoemd de eigenwaarde van A corresponderen met V.

Alle eigenwaarden en eigenvectoren voldoen aan de vergelijking bijl = λx voor een gegeven vierkant matrix A.

De online Eigenvectors en EigenValues ​​Calculator kunnen | een |, enkelvoudige matrix (A - C × I), trace van A, Eigen-waarde van de matrix A

Bijvoorbeeld

Voor matrix

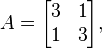
de vector

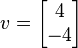
is een eigenvector met EigenValue 2.

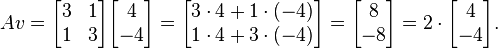
Aan de andere kant de vector

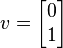
is niet een eigevector, sindsdien

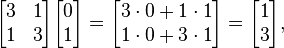
En deze vector is geen veelvoud van de originele vector v.

Eigenvectoren en eigevalues ​​berekening
Aanbeveling rekenmachines Resolver desigualdades lineares Calculadora de distribuição hipergeométrica Calculadora de equação sexta Calculadora científica online. Efeito da calculadora de tamanho Equações de Transposição Resolvendo a calculadora Sinal para a calculadora de relação de ruído Calculadora do produto Cruz do vetor Calculadora de adição de vetor Calculadora de convolução online. Soma de calculadora consecutiva cubos Soma de calculadora de praças Soma de calculadora de quadrados consecutivos Calculadora de conjuntos de diferença simétrica Calculadora de teorema binômio