FoxCalculators - Gratis rekenmachines online!

Η εκθετική αποσύνθεση / ανάπτυξη είναι πολύ χρήσιμη στα mathmatics. Η εκθετική αποσύνθεση εμφανίζεται όταν ο ρυθμός ανάπτυξης είναι αρνητικός. Η εκθετική ανάπτυξη με τον ίδιο τρόπο συμβαίνει όταν ο ρυθμός ανάπτυξης της αξίας μιας μαθηματικής λειτουργίας είναι ανάλογος με την τρέχουσα τιμή της λειτουργίας.

Ο τύπος για την εκθετική ανάπτυξη μιας μεταβλητής X με τον (θετικό ή αρνητικό) ρυθμό ανάπτυξης R, όσο το χρόνο t συνεχίζεται σε διακριτά διαστήματα (δηλαδή, σε ακέραιους χρόνους 0, 1, 2, 3, ...), είναι < b> x _{t = x 0 (1 + r)}

Όπου x _{0 είναι η τιμή του Χ εγκαίρως 0. Όταν το R είναι αρνητικό itis εκθετική αποσύνθεση, όταν το R είναι θετικό, είναι εκθετική ανάπτυξη. Για παράδειγμα, ο ρυθμός ανάπτυξης του R = 5% = 0,05, που πηγαίνει από οποιαδήποτε ακέραια τιμή χρόνου στον επόμενο ακέραιο αιτίες X τη δεύτερη φορά να είναι 1,05 φορές τι ήταν η προηγούμενη φορά.}

Για παράδειγμα, r = -0,5, το γράφημα θα μειωθεί (decaying). Κάθε φορά το t αυξάνεται κατά 1, το x _{t μειώνεται στο ήμισυ της προηγούμενης τιμής του.}

Όταν r = 1, το γράφημα θα είναι ανάπτυξη. Κάθε φορά το t αυξάνεται κατά 1, x _{t αυξάνεται κατά ένα συντελεστή 2.}

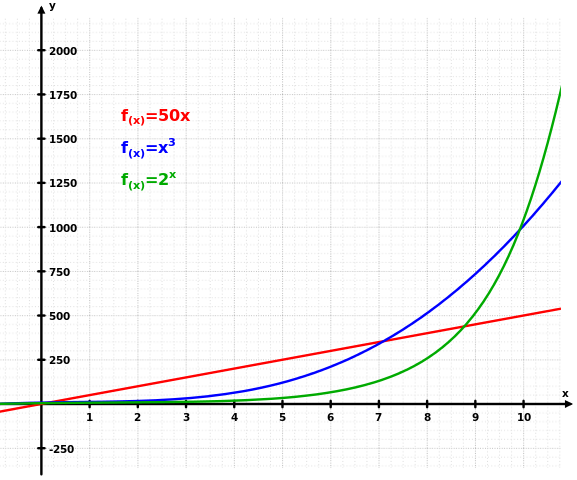
Το γράφημα απεικονίζει τον τρόπο με τον οποίο η εκθετική ανάπτυξη (πράσινο) ξεπερνά τόσο τη γραμμική (κόκκινη) όσο και κυβική (μπλε) ανάπτυξη.