Υπολογισμός EigenValues ​​και Eigenvalues

Regular Matrix A =
Identity Matrix I =
Scalar Matrix(Z=c×I)
c =
|A| =
Singular Matrix (A - c×I) =
|A - c×I| =
Trace of A =
Eigen Value (c2) =
Eigen Value (c1) =
c1 in Eigen Vector x1 value =
c2 in Eigen Vector x1 value =
c1 in Eigen Vector x2 value =
c2 in Eigen Vector x2 value =

Ένας ιδιοτιμέας ενός τετραγωνικού μήτρα Α είναι ένας μη μηδενικός φορέας V, όταν ένα V = λ V, το λ ονομάζεται Eigenvalue ενός αντίστοιχου σε v.

Όλες οι ιδιοτιμές και οι ιδιοτιμώνες ικανοποιούν την εξίσωση AX = ΛΧ για ένα δεδομένο τετράγωνο μήτρα Α.

Οι σε απευθείας σύνδεση αίθουσες EigenVectors και Eigenvalues ​​μπορούν να πάρουν | α |, μοναδική μήτρα (a - c × i), ίχνος μιας αξίας A, Eigen της Matrix A

Για παράδειγμα

Για τη μήτρα

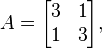
ο φορέας

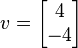
είναι ένας ιδιοτιμέας με την Eigenvalue 2.

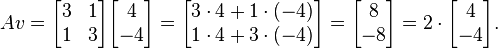
Από την άλλη πλευρά ο φορέας

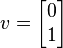
είναι όχι ένας ιδιοτιμέας, από τότε

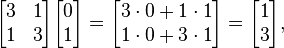
Και αυτός ο φορέας δεν είναι πολλαπλάσιος από τον αρχικό διάνυσμα v.

Υπολογισμός EigenValues ​​και Eigenvalues
Aanbeveling rekenmachines Resolver desigualdades lineares Calculadora de distribuição hipergeométrica Calculadora de equação sexta Calculadora científica online. Efeito da calculadora de tamanho Equações de Transposição Resolvendo a calculadora Sinal para a calculadora de relação de ruído Calculadora do produto Cruz do vetor Calculadora de adição de vetor Calculadora de convolução online. Soma de calculadora consecutiva cubos Soma de calculadora de praças Soma de calculadora de quadrados consecutivos Calculadora de conjuntos de diferença simétrica Calculadora de teorema binômio