Cartesiaanse vergelijking van een vliegtuigcalculator

Point A , ,
Point B , ,
Point C , ,
   
Equation of the plane
(given three points)		 x+y+z+=0

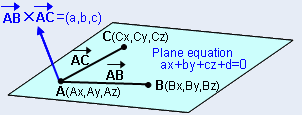
Er zijn drie punten A (x 1 , y 1 , z 1 ), B (x 2 , y 2 , z 2 ) en C (x 3 , y 3 , z 3 ) Liggend in een vliegtuig, dan kan de vlakvergelijking worden gevonden met behulp van de volgende formule

X - X 1

Y - Y 1

Z - Z 1

= 0

X 2 - X 1

Y 2 - Y 1

Z 2 - Z 1

X 3 - X 1

Y 3 - Y 1

Z 3 - Z 1

Of een (AX, AY, AZ), B (BX, BZ, BZ), C (CX, CY, CZ), de vergelijking van het vlak is bijl + door + cz + d = 0

Waar,

A = (BY-AY) (CZ-AZ) - (CY-AY) (BZ-AZ)

B = (BZ-AZ) (CX-AX) - (CZ-AZ) (BX-AX)

C = (BX-AX) (CY-AY) - (CX-AX) (bij-AY)

D = - (AAX + BAY + CAZ).

Cartesian Vlak-vergelijking Berekening met de drie coördinaten wordt hier gemakkelijker gemaakt.

Cartesiaanse vergelijking van een vliegtuigcalculator
Aanbeveling rekenmachines Resolver desigualdades lineares Calculadora de distribuição hipergeométrica Calculadora de equação sexta Calculadora científica online. Efeito da calculadora de tamanho Equações de Transposição Resolvendo a calculadora Sinal para a calculadora de relação de ruído Calculadora do produto Cruz do vetor Calculadora de adição de vetor Calculadora de convolução online. Soma de calculadora consecutiva cubos Soma de calculadora de praças Soma de calculadora de quadrados consecutivos Calculadora de conjuntos de diferença simétrica Calculadora de teorema binômio