Αριθμομηχανή

r₁ =
r₂ =
Units:

C₁ =	0
C₂ =	0
A₁ =	0
A₂ =	0
A₀ =	0

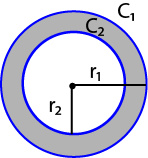
annulus

r _{1 = εξωτερική ακτίνα}

r _{2 = εσωτερική ακτίνα}

C _{1 = εξωτερική περιφέρεια}

C _{2 = εσωτερική περιφέρεια}

Μια _{1 = περιοχή του κύκλου του r ₁}

Ένα _{2 = περιοχή του κύκλου του r ₂}

Μια _{0 = σκιασμένη περιοχή}

Ο σε απευθείας σύνδεση ακτινοβολεί τον αριθμομηχανή για να βρει την περιοχή, την περιφέρεια και την ακτίνα ενός δακτυλίου. Όταν γνωρίζετε δύο γνωστές μεταβλητές και, στη συνέχεια, επιλέξτε από το Droplist, υπολογίστε τα άλλα 5 άγνωστα.

Τύποι τύπων:

δεδομένου r _{1 και r _{2 :}}

C _{1 = 2πρ ₁}

C _{2 = 2πρ ₂}

A _{1 = β _{1 ²}}

A _{2 = β _{2 ²}}

Ένα _{0 = a _{1 - a _{2 .}}}

δεδομένου r _{1 and c _{2 :}}

r _{2 = c _{2 / 2π}}

C _{1 = 2πρ ₁}

A _{1 = β _{1 ²}}

A _{2 = β _{2 ²}}

Ένα _{0 = a _{1 - a _{2 .}}}

δεδομένου r _{1 και a _{2 :}}

r _{2 = √ (a _{2 / π)}}

C _{1 = 2πρ ₁}

C _{1 = 2πρ ₂}

A _{1 = β _{1 ²}}

Ένα _{0 = a _{1 - a _{2 .}}}

δεδομένου r _{2 and c _{1 :}}

r _{1 = c _{1 / 2π}}

C _{2 = 2πρ ₂}

A _{1 = β _{1 ²}}

A _{2 = β _{2 ²}}

Ένα _{0 = a _{1 - a _{2 .}}}

Λαμβάνοντας c _{1 και c _{2 :}}

r _{1 = c _{1 / 2π}}

r _{2 = c _{1 / 2π}}

A _{1 = β _{1 ²}}

A _{2 = β _{2 ²}}

Ένα _{0 = a _{1 - a δεδομένου c _{1 και a _{<<<< / sub> :}}}}

r _{1 = c _{1 / 2π}}

r _{2 = √ (a _{2 / π)}}

C _{2 = 2πρ ₂}

A _{1 = β _{1 ²}}

Ένα _{0 = a _{1 - a _{2 .}}}

Λαμβάνοντας υπόψη το r _{2 και a _{1 :}}

r _{1 = √ (a _{1 / π)}}

C _{1 = 2πρ ₁}

C _{2 = 2πρ ₂}

A _{2 = β _{2 ²}}

Ένα _{0 = a _{1 - a _{2 .}}}

δεδομένου c _{2 και a _{1 :}}

r _{1 = √ (a _{1 / π)}}

r _{2 = c _{2 / 2π}}

C _{1 = 2πρ ₁}

A _{2 = β _{2 ²}}

Ένα _{0 = a _{1 - a _{2 .}}}

Λαμβάνοντας ένα _{1 και a _{2 :}}

r _{1 = √ (a _{1 / π)}}

r _{2 = √ (a _{2 / π)}}

C _{1 = 2πρ ₁}

C _{2 = 2πρ ₂}

Ένα _{0 = a _{1 - a _{2 .}}}

δεδομένου r _{1 και a _{0 :}}

C _{1 = 2πρ ₁}

A _{1 = β _{1 ²}}

Ένα _{2 = a _{1 - a ₀}}

r _{2 = √ (a _{2 / π)}}

C _{2 = 2πρ _{2 .}}

δεδομένου r _{2 και a _{0 :}}

C _{2 = 2πρ ₂}

A _{2 = β _{2 ²}}

Ένα _{1 = a _{0 + a ₂}}

r _{1 = √ (a _{1 / π)}}

C _{1 = 2πρ _{2 .}}

δεδομένου c _{1 και a _{0 :}}

r _{1 = c _{1 / 2π}}

A _{1 = β _{1 ²}}

Ένα _{2 = a _{1 - a ₀}}

r _{2 = √ (a _{2 / π)}}

C _{2 = 2πρ _{2 .}}

δεδομένου c _{2 και a _{0 :}}

r _{2 = c _{2 / 2π}}

A _{2 = β _{2 ²}}

Ένα _{1 = a _{0 + a ₂}}

r _{1 = √ (a _{1 / π)}}

C _{1 = 2πρ _{1 .}}

Λαμβάνοντας ένα _{1 και a _{0 :}}

Ένα _{2 = a _{1 - a ₀}}

r _{1 = √ (a _{1 / π)}}

r _{2 = √ (a _{2 / π)}}

C _{1 = 2πρ ₁}

C _{2 = 2πρ _{2 .}}

Λαμβάνοντας ένα _{2 και a _{0 :}}

Ένα _{1 = a _{0 + a ₂}}

r _{1 = √ (a _{1 / π)}}

r _{2 = √ (a _{2 / π)}}

C _{1 = 2πρ ₁}

C _{2 = 2πρ _{2 .}}

Αριθμομηχανή

FoxCalculators - Gratis rekenmachines online!

Αριθμομηχανή

Τύποι τύπων: